N 个分支的树。

遍历

跟 二叉树 类似，区别点在于：

• 二叉树是左右子节点，N-ary 树是若干 children 节点
• N-ary 没有中序遍历，因为有无数种所谓「中序」，比如 (child1, root, chid2, child3, ...)

下面的代码以这颗树作为测试用例：

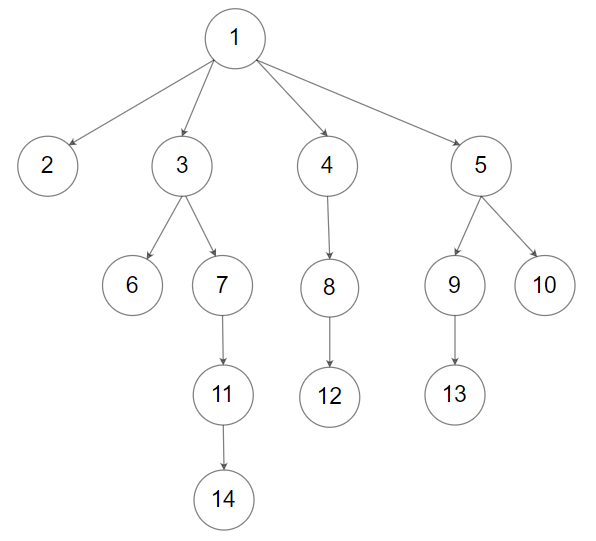
中序遍历、后序遍历、按层遍历的实现：

package main

import "fmt"

type Node struct {
	Val      int
	Children []*Node
}

func preorder(root *Node) []int {
	answer := []int{}
	if root == nil {
		return answer
	}

	stack := []*Node{root}
	for len(stack) != 0 {
		curr := stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		answer = append(answer, curr.Val)
		for i := len(curr.Children) - 1; i >= 0; i-- {
			stack = append(stack, curr.Children[i])
		}
	}

	return answer
}

func postorder(root *Node) []int {
	answer := []int{}
	if root == nil {
		return answer
	}

	firstStack := []*Node{root}
	secondStack := []*Node{}

	for len(firstStack) != 0 {
		curr := firstStack[len(firstStack)-1]
		firstStack = firstStack[:len(firstStack)-1]

		secondStack = append(secondStack, curr)
		firstStack = append(firstStack, curr.Children...)
	}

	for len(secondStack) != 0 {
		answer = append(answer, secondStack[len(secondStack)-1].Val)
		secondStack = secondStack[:len(secondStack)-1]
	}
	return answer
}

func levelOrder(root *Node) [][]int {
	answer := make([][]int, 0)
	if root == nil {
		return answer
	}

	queue := []*Node{root}

	for len(queue) != 0 {
		levelAnswer := []int{}
		nextQueue := []*Node{}
		for _, node := range queue {
			levelAnswer = append(levelAnswer, node.Val)
			nextQueue = append(nextQueue, node.Children...)
		}
		queue = nextQueue
		answer = append(answer, levelAnswer)
	}

	return answer
}

func main() {
	root := &Node{
		1, []*Node{
			{2, nil},
			{3, []*Node{
				{6, nil},
				{7, []*Node{
					{11, []*Node{
						{14, nil},
					}},
				}},
			}},
			{4, []*Node{
				{8, []*Node{
					{12, nil},
				}},
			}},
			{5, []*Node{
				{9, []*Node{
					{13, nil},
				}},
				{10, nil},
			}},
		},
	}
	fmt.Println(preorder(root))
	fmt.Println(postorder(root))
	fmt.Println(levelOrder(root))
}